

Of course, it's also helpful to be able to check your work. Therefore, a = − 2 a = -2 a = − 2 and b = − 15 b = -15 b = − 15.Īnd that's all there is to it! Be sure to practice all of these concepts to master the remainder and factor theorems. Using the Factor Theorem, test and see which of the following binomials are factors of the polynomial: A binomial factor is simply a factor with two terms, like (x - 4). Note, to factor polynomials, the factors we get are often referred to as "binomials". The best way to understand the methodology behind factor theorem is to do some factor theorem examples. If the remainder of such a division is not zero, then (x - c) is not a factor. Thus, according to this theorem, if the remainder of a division like those described above equals zero, (x - c) must be a factor. If we divide a polynomial f(x) by (x - c), and (x - c) is a factor of the polynomial f(x), then the remainder of that division is simply equal to 0. In the factor theorem, we use this same concept to prove the following: According to the Factor Theorem:
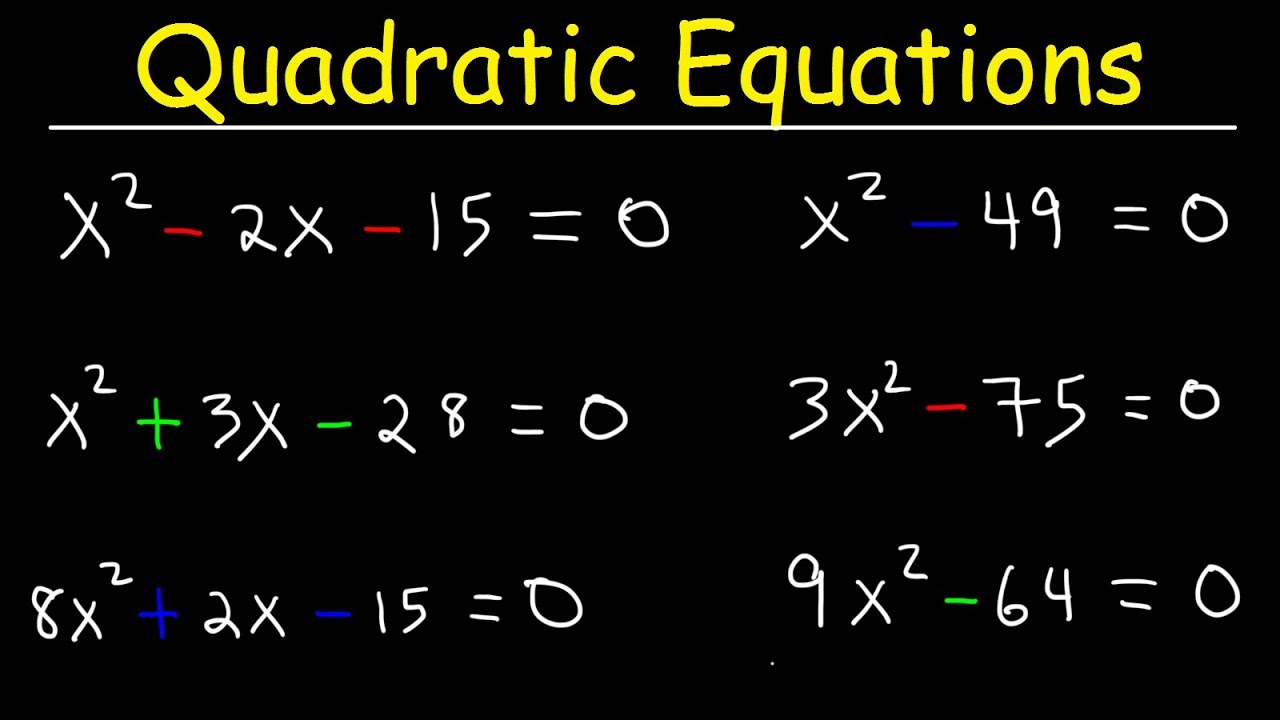
Recall, that in the remainder theorem, if we divide a polynomial f(x) by (x-c), the remainder of that division is simply equal to f(c).
In its most basic terms, the factor theorem really is just a special case of the remainder theorem. 7 is not a factor of 20 because, when 20 is divided by 7, we get 2.86, which is not a whole number (this is the same as saying 2 and a remainder of 0.86). In its simplest terms, consider the following: 4 is a factor of 20 because, when 20 is divided by 4, we get the whole number 5 and no remainder. With regards to division, a factor is just a term or expression that, when another term or expression is divided by this factor, the remainder is equal to zero. The understanding of what factors are is crucial to all of mathematics, and it is a term you will hear again and again as you progress with your studies. Now that we have an understanding of the remainder theorem, the last little thing we must understand before moving onto the factor theorem is what exactly a "factor" is. In addition, a review on the concepts behind the remainder theorem, as well as a visual proof of the theorem, is also helpful. But, in any case, our lessons on synthetic division and long division of polynomials will help you understand factor theorem better. Without this theorem, we would have to go to the trouble of using long division and/or synthetic division to solve for the remainder, which is difficult and time consuming. This theorem is especially helpful because it reduces the amount of work we have to do to solve these types of problems. If we divide a polynomial f(x) by (x - c), the remainder of that division is simply equal to f(c). One can't exist without the other, so it is very important that we define what the remainder theorem is before getting into the factor theorem.
The remainder theorem and factor theorem are very closely related concepts in mathematics. Before getting into the Factor Theorem and what it means, it is crucial that we fully understand the Remainder Theorem and what factors are first.


 0 kommentar(er)
0 kommentar(er)
